Modeling With Data

Moore's law won't save you

PDF version

First, let's get Moore's law straight: According to Gordon Moore himself, the law is that “the complexity for minimum component costs has increased at a rate of roughly a factor of two per year.” The press typically translates that to English to say that every year you can buy about twice as much memory for your PC for your dollar.

It's just about true: measures of the PC memory market's megabytes per dollar typically double about every two years.

But that's not what people want from Moore's law. They want to say that their PCs run faster. Memory is nice--more memory means more windows open in your browser--but it doesn't immediately translate to zippier computing in its various forms, such as more complex processes and on-the-fly behavior that used to be background behavior.

No, for that, you just need a faster processor, which partly depends on having cheaper components, and partly on better design.

Here's what I did for this little demonstration: first, I asked Wikipedia for a table of processors and their posted speeds. Processor speeds are measured in millions of instructions per second--MIPS, though by an instruction we mean a computer instruction like `shift that bit to the left', and it takes several thousand such instructions to execute a human instruction like `divide 13 by 8'.

Then, I divided each processor's MIPS by the number of cores in the processor. I'll talk about cores next time if you're not familiar with them. Then I used the best score for the year as the data point to plot.

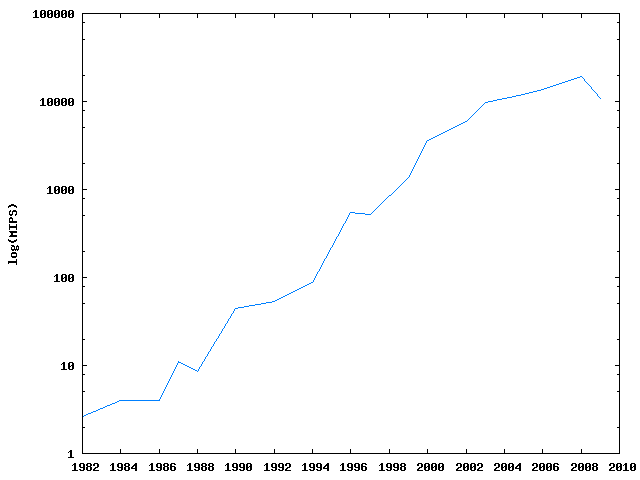
Figure One: Processor speed continues to progress, but not at its former pace.

This is a logarithmic scale, meaning that what looks like a line here is actually exponential growth, from the Intel 286 in `82, at 2.6 MIPS, to the Intel Core i7 Extreme 965EE, which justifies its absurd name by running 19,095 MIPS.

That's certainly amazing progress. For much of the period, it's doubling even faster than every year. In 1994, the fastest retail chip (Motorola 68060, used in MacIntoshes) ran at 88 MIPS, the fastest retail chip two years later (Intel Pentium Pro) ran at 541 MIPS--more than six times faster in two years.

But then things flatten out. The fastest in 2003 was 9,700 MIPS; the fastest in 2008 was 19,095 MIPS, so the doubling of speeds took five years instead of several months.

Caveats

I suppose I should mention the trouble with MIPS. First, how do you measure a processor's MIPS? Answer: using the processor's clock to time itself doing things. So you already have potential for shenanigans. If Motorola's definition of `instruction' differs from Intel's, it may be hard to compare MIPS across them.

And there's more to zippy processing than just summing numbers. Much of the work is in retrieving data and instructions, which can take a lot of time. After all, the computer's memory and the processor are often separated by several centimeters. More importantly, there needs to be a component (a bus) doing traffic control and getting the right bits to the right place. All that takes time. One solution is to have a local space on the processor itself that keeps copies of what is expected to be the most useful data, which is why the typical modern PC processor has a hierarchy of increasingly fast Level 1, Level 2, and sometimes Level 3 data caches. According to the Slate article linked from Gordon Moore's name above, that's why Figure one shows a drop in 2009: Intel decided to spend more transistors on memory and power-saving, and fewer on fancy calculating tricks. They seem to expect that that'll make for a more pleasant computing experience for most users, and I'm willing to believe them.

So there are a lot of ways to make a computer go faster than just more math per second; I could list a dozen of them here, but that might be off topic. This is a blog about computational statistics, so all of those great advances don't matter for our purposes as much as the simple question of how many times the system can make a random draw from a Normal distribution.

I'll continue on this thread, and add even more caveats, next time. But all the caveats aside, I believe the story from the figure is basically true: the era of immense speed gains is over, or is at least currently in a lull. We're certainly progressing, and next year's PC will be faster than this year's, but it won't be ten times faster or even twice as fast. In the mid 1990s, if a program ran too slowly, we could just wave it off and say that next year's computer will run it just fine, but we can't do that anymore.

[Previous entry: "Today, I am a blog."]
[Next entry: "Parallels II"]