Modeling With Data

Easy re-typing with designated initializers

PDF version

This column is about dealing with multiple formats for the same thing. To give the simplest example, consider a plain old list of numbers. The raw representation is an array, where the numbers are a sequence in memory. But then you don't know how long the thing is, so you need to also have a note somewhere as to its size. Maybe you want to name it, or treat it like 2-D matrix. Next thing you know, you've got a long list of extra data taped to that simple list.

Now you've got design problems. In terms of the systems I work with, you've got several levels of intent and complexity, including the simple double *, the gsl_vector*, the gsl_matrix*, and the apop_data* structures, any of which could be used to represent a few numbers.

These different structures aren't just there for fun: a scalar doesn't necessarily behave like a 1×1 matrix or a one-unit vector.

• a scalar times a N×1 column vector is usually read to produce a scaled N×1 vector.
• A 1×1 matrix ⋅ a N-unit vector is a similar scaling operation, but here we'll have to assume that the vector is a row vector, and the output will be either a 1×N matrix or a N-element vector understood to be a row, depending on custom.
• A vector dot a vector is usually taken to mean a row vector x dot a column vector y, producing x₁y₁ + x₂y₂ + ... + x_ny_n. But a vector of length one doesn't match dimensions with a vector of length N > 1, so in this case we'd just throw an error.

There are already a lot of subtleties, like whether we want to be explicit about whether a vector is a row or a column, or just assume that it'll do whatever is needed to conform, or whether the output wants to be a scalar, vector, or matrix.

Dealing with complexity

These different, sort of overlapping types are necessary, but they inevitably add complexity to the system. There are some methods for dealing with these different types, all of which have their benefits and bugs.

• Just make everything the most inclusive structure. Pros: users don't have to think: everything is a named N-dimensional frame of long long double-precision floating-point numbers, labeled with arbitrary-length strings, and there's no need to worry about sub-types and such. Cons: writing down the number 14 is now a massive production. Now you couldn't distinguish a scalar from a 1×1 matrix if you wanted to.
• Overload functions, so a function can take any representation of a list of numbers as input, and handles the differences internally. This gives surface ease, because the function user usually doesn't have to think too hard about types. But if it's a double* you still need to remember to send in an extra length parameter, and it's hard to encode the above scalar/vector/matrix subtleties into such a system, because you're never quite sure how a function will read your inputs. The bugs produced by subtle differences like these are, in my experience, among the most difficult to debug.
• Have the user do the type-casting between things: pulling smaller elements out of the larger structs, and building purpose-built parent structures to wrap the smaller stuff. Cons: you need to know the structures, and have to do the work of explicitly stating things. Pros: the process of subsetting takes zero computer time, and the process of wrapping is not necessarily annoying, as discussed below.

None of these methods are ideal, and which devil you choose is a matter of local considerations, practical issues, and personal taste. I gravitate toward the third, wherein the user is expected to know the darn underlying hierarchy of types, and deal accordingly. Why? Because I've found that systems that hide that hierarchy from you do a lousy job of it. In case this essay isn't long enough, have a look at this essay on the law of leaky abstractions, which explains that you can get away with not explicitly acknowledging the different types for a while, but eventually you're going to have to confront the differences. With good technique, it's not hard to switch types on the fly.

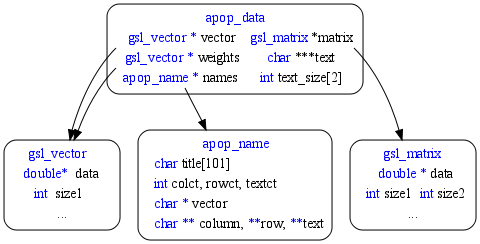
Figure One: The double* to gsl_matrix/_vector to apop_data hierarchy.

Making it easy

Getting elements out of a structure is pretty easy: just point to it. Because you can have multiple pointers pointing to the same thing, it's easy to rename something that is deeply nested inside the hierarchy. E.g., an apop_model (which would float above the type diagram above) holds parameters in an apop_data set, which holds a gsl_vector, which holds a list of doubles. So:

double *list = my_model->parameters->vector->data;
do_something(list);
do_more(list[3]);

Since the new name is just a spare pointer to the same data, all changes to the data (without moving the pointers themselves) happen as expected, you didn't copy any data, and you don't have to free anything at the end. Clean and simple.

Going up the hierarchy is more difficult, because you need to add all that extra data yourself; one paragraph was enough to cover going down the tree, and the rest of this column will be about going up the tree. I'll start from the most verbose, and work my way toward the easier methods, so don't get discouraged by the part where I use ten lines to take a dot product--I'll have it back down to one in the end. As we C users like to say, there are an infinite number of ways to do it.

There are functions to wrap things. For example, the apop_dot function has a quite clean syntax that takes in two apop_data structs (plus optional parameters indicating transposition), but if your data isn't in that input format, you'll need to wrap it. Here's an example where we know that we're multiplying a 3×2 matrix against a two-element column vector, using a function to copy data to the right structure:

apop_data *a_dot(double *set1, double *set2){
    apop_data *d1 = apop_line_to_data(set1, 0, 3, 2);
    apop_data *d2 = apop_line_to_data(set2, 2, 0, 0);
    apop_data *out = apop_dot(d1, d2);
    apop_data_free(d1);
    apop_data_free(d2);
    return out;
}

If you're just doing this once, the deallocations at the end may be optional, but if you're writing a function to be called a million times, they'll become essential.

For matrices or vectors, you could produce a dummy wrapper and then point to the data. But don't forget to unlink before calling the free function, lest you lose the original data:

apop_data *another_dot(gsl_vector *v, gsl_matrix *m){
    apop_data *dummy1 = apop_data_alloc(0,0,0);
    apop_data *dummy2 = apop_data_alloc(0,0,0);
    dummy1->vector = v;
    dummy2->matrix = m;
    apop_data *out = apop_dot(dummy1, dummy2);
    dummy1->vector = NULL;
    dummy1->matrix = NULL;
    apop_data_free(dummy1);
    apop_data_free(dummy2);
    return out;
}

That is unabashedly a lot of work for one dot product.

The first way in which we can save the trouble of deallocating is to use the static keyword to guarantee that a shell will always be on hand to fill. If you're not familiar with static variables, see pp 39-40 of Modeling with Data.

I do this sort of thing so often that I even have a convenience macro to simplify the process.

#define Staticdef(type, name, def) static type name = NULL; \
                                    if (!(name)) name = def;

apop_data *easier_dot(gsl_vector *v, gsl_matrix *m){
    Staticdef(apop_data*, dummy1, apop_data_alloc(0,0,0));
    Staticdef(apop_data*, dummy2, apop_data_alloc(0,0,0));
    dummy1->vector = v;
    dummy2->matrix = m;
    return apop_dot(dummy1, dummy2);
}

The next step in the chain is to just produce that dummy structure on the fly, which is where designated initializers come in.

apop_data *easiest_dot(gsl_vector *v, gsl_matrix *m){
    apop_data dummy1 = {.vector = v};
    apop_data dummy2 = {.matrix = m};
    return apop_dot(&dummy1, &dummy2);
}

What just happened: we used designated initializers p 32 of Modeling with Data to allocate a structure and fill one element. The elements not explicitly mentioned are zero, so we don't have to worry about them. This works for the apop_data structure because it is designed to be OK with being mostly empty; below we'll see some structures that are a bit more needy.

That trick allocated an apop_data struct, but you'll notice that every library function takes in a pointer: apop_data*. This distinction is why we need to use &dummy1 instead of just dummy1 when making the function call. But this setup means that we don't have to deallocate anything at the end: the structure is cleaned up automatically when the function exits.

Some people are lines-of-code averse, and really hate the idea of having those extra lines of code producing extra structures. So, just do it in place:

apop_data *one_line_dot(gsl_vector *v, gsl_matrix *m){
    return apop_dot(&((apop_data) {.vector = v}), &((apop_data) {.matrix = m}));
}

I like the three-line form better, myself, partly because I need the (apop_data) type cast when not on the declaration line. Maybe some macros will clean up the second form:

#define d_from_v(v) &((apop_data) {.vector = v})
#define d_from_m(m) &((apop_data) {.matrix = m})

apop_data *one_line_dot(gsl_vector *v, gsl_matrix *m){
    return apop_dot(d_from_m(m), d_from_v(v));
}

Going from a raw array to the GSL's vectors and matrices require a little more care, because you'll need to add some metadata: the number of rows/columns, and the requisite jumps.

apop_data *a_dot_again(double *set1, double *set2){
    gsl_vector m = {.data = set1, .size1=3, .size2=2, .tda = 3};
    gsl_vector v = {.data = set2, .size=2, .stride = 1};
    return apop_dot(d_from_m(m), d_from_v(v));
}

The tda (trailing dimension of array) and stride elements tell the system how to convert the 1-D layout in memory into the right shape. For subvectors and submatrices, the jumps may take different forms, but for our purposes, the tda is always equal to the row size, and the stride is always one. With that in mind, we can wrap these details in macros, and daisy-chain it all together:

#define v_from_a(v, size) &((gsl_vector) {.data = (v),\
                      .size =(size), .stride = 1})
#define m_from_a(m, size1, size2) &((gsl_matrix) {.data = (m),\
                      .size1 =(size1), .size2=(size2), .tda = (size1)})

apop_data *a_dot_again(double *set1, double *set2){
    return apop_dot(d_from_m(m_from_a(set1, 3, 2)), d_from_v(v_from_a(set2, 2)));
}

In the end, you're still going to have to climb your way up the hierarchy a few steps for this array-to-data case to work. It's up to you if you want to take that last step and write a more macros:

#define dv_from_a(a, size) d_from_v(v_from_a(a, size))
#define dm_from_a(a, size1, size2) d_from_m(m_from_a(a, size1, size2))

All of these macros are cheap, in the sense that they allocate short structures and don't copy any of your data. Also, they're a whole lot shorter than the ten-line version.

On the con side, I think there exist people who would call them bad style, because you're not using the formal methods of allocation (e.g., gsl_vector_alloc), and are thus bypassing checks that things are OK. Situations that depend on those ignored structure elements having non-NULL values may surprise you in odd cases.

There's the problem that by skipping the setter functions, you're assuming knowledge of the internal structure of the struct that shouldn't be your problem--which is true: you the user shouldn't really have to care about tdas. At least you can look those details up once and hide them in a macro. This argument usually continues that the underlying structures might change as the designers come up with new ideas, but this is not seriously an issue. Early on, structures change, but at this point, the GSL and even Apophenia have a sufficiently large base of users that arbitrarily screwing around with core structures is a social impossibility. So, frankly, the macros here are not as bad form as the textbooks say they are.

Summary paragraph: There's real benefit to having different types: a scalar is just not a 1×1 matrix or a one-item vector, so we need to be able to specify all these structures. But, as a direct corollary, we need to be able to easily jump between structures as necessary. In this column, I gave you nine examples of how to take a dot product, depending on the inputs. Our pals designated initializers and compound literals saved the day, because they let us set up a quick structure, fill it, and use it without worrying about memory and deallocation. You can apply these tricks in a variety of situations; for those of you who might follow exactly the array-to-matrix-to-data forms above, here are all the macros I used in one cut-and-pasteable block:

#define Staticdef(type, name, def) static type name = NULL; if (!(name)) name = def;

#define d_from_v(v) &((apop_data) {.vector = (v)})
#define d_from_m(m) &((apop_data) {.matrix = (m)})

#define v_from_a(v, size) &((gsl_vector) {.data = (v), .size =(size), .stride = 1})
#define m_from_a(m, size1, size2) &((gsl_matrix) {.data = (m), .size1 =(size1), .size2=(size2), .tda = (size1)})

#define dv_from_a(v, size) d_from_v(v_from_a(v, size))
#define dm_from_a(m, size1, size2) d_from_m(m_from_a(m, size1, size2))

[Previous entry: "Computing history and its scars"]
[Next entry: "Yet another git tutorial"]